Leo Amino, “Refractional #85” (1972)
Leo Amino background
Leo Amino is the first artist in the United States to use plastics as a principal medium for experiment. He is responsible for the innovation of cast plastics in the history of modern sculpture. Inspired in part by the Plexiglas experiments of the Russian Constructivists as well as Bauhaus sensibilities, his embrace of light and colour as primary elements of sculptural construction anticipated the work of avant-garde American artists in the 1960s, some of whom had been his students. Amino shared a resolutely anti-conformist and anti-traditionalist philosophy with the exiles and refugees of the Bauhaus. Like fellow experimentalists of his generation Josef Albers and Ad Reinhardt, Amino was initially recognized by the cooperative Artists’s Gallery, where he received his first solo exhibition in 1940. After several one-man shows in New York, Amino was invited by Albers to join the faculty of Black Mountain College in the summer of 1946, two years after the college’s integration, where he taught alongside the Albserses, Jacob Lawrence, and Walter Gropius, and informed the education of students Ruth Asawa, Kenneth Noland, and Harry Seidler, among others. The first artist in the United States to utilize plastics as a principal material, Amino pioneered this medium more than two decades before its widespread use by other American artists, making him the successor to the Plexiglas experimentations of Bauhaus and constructivist artists Naum Gabo and László Moholy-Nagy. The artist’s experiments emerged from dissatisfaction with his attempts to incorporate colour into traditional sculptural media, anticipating the concerns of minimalist artists that would not gain widespread attention until the 1960s. Amino dedicated the second half of his career exclusively to these ideas, producing a series of “refractional” compositions with light, colour, and transparency.*
Imagining a 3D sonic space
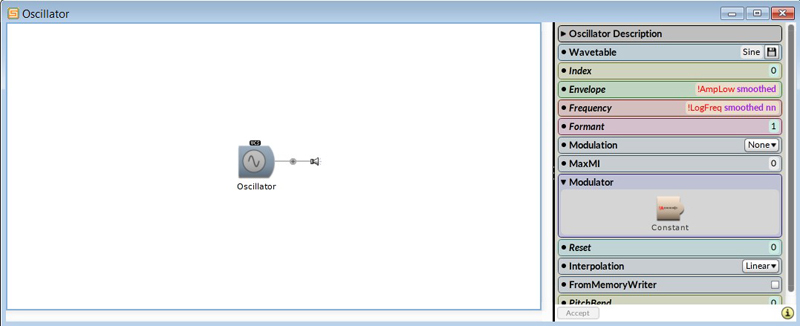
This waveform is shown here with an oscilloscope:
By adding several sine waves with different frequencies and their different amplitudes, powerful spectral sound towers can be built. The energy of eight sine waves with the same frequency. Each sine waveform is generated by a single oscillator. Taken together, they can form certain timbres. It all depends on which frequencies and their amplitude are stacked on top of each other.
A stack of sixteen sine waves, added step by step, produces different frequency patterns as towers of timbres by changing the amplitudes and frequencies.
Noise and spectra
White noise refers to a sound that contains all frequencies of the spectrum of audible sound equally. White noise has the same amount of energy in each frequency band. When we look at the spectrum of white noise, it appears flat or even across all frequencies because it has the same energy for all frequencies. Every single frequency is a sine wave.
Pink noise has the same energy in the same pitch ranges. Therefore, pink noise sounds more low-pass filtered and darker than white noise. The frequency spectrum is such that the power spectral density is inversely proportional to the frequency of the signal: 1/f noise.
Creation of frequency bands
Just as Leo Amino chose his materials, We too must choose which form(s) of sound to use for this project. We have to create sound structures that can be open or clustered as material on a molecular level. :Below we find the original colours in frequency bands:
|
yellow |
507-526 THz |
570--591 nm |
|
red |
400–484 THz |
620–750 nm |
|
blue |
606–630 THz |
476–495 nm |
Noise bands are created by using white noise that passes through a comb filter. This type of filtering is created by mixing the original signal with a delayed version of the original signal. This type of mixing, adds frequencies and removes some frequencies.
The structure of the comb filter:
Noise is added to itself by delaying 16 samples, creating bands as we see in the
next figure. The noise bands are formed by changing the delay:
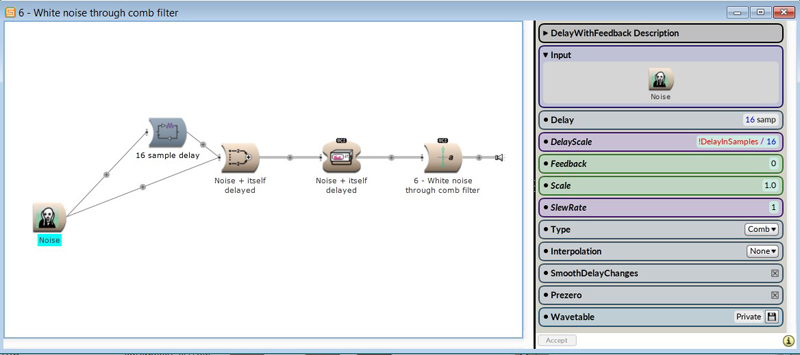
The sample delay corresponds to the partial. A partial is a non-fundamental tone that is multiplied by a fraction, not by integers. If we increase the number of samples, there are more bands for the noise to run through:
The same principle is used in the creation of band-pass filters. With bands
corresponding to colour frequencies divided into the audio spectrum.
Noise band with frequencies for yellow:
Noise band with frequencies for red:
The term red noise is used for Brownian noise. For artistic reasons I use
this term here as the distribution in the original colour spectrum above.
Noise band with frequencies for blue:
Different ways to approach Noise
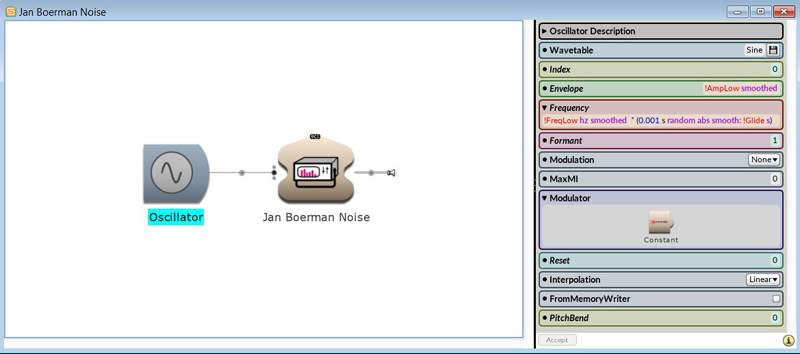
The colour of the spectrum follows the increasing random modulation signal:
In the extended version we can specify further parameters to shape this randomness and introduce Brownian noise:
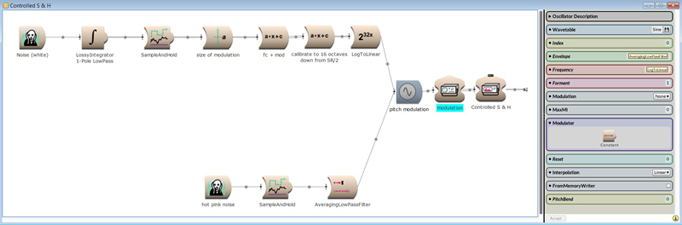
These parameters are a better tunable Brownian random modulation signal for the frequency of the oscillator and a white noise random modulation signal for the amplitude of the oscillator. In this example, both the frequency and the amplitude are modulated:
Brownian noise
A white noise with a derived feedback decay as a function of a Brownian motion. Brownian motion explores the environment. A delay module can be considered as a space.
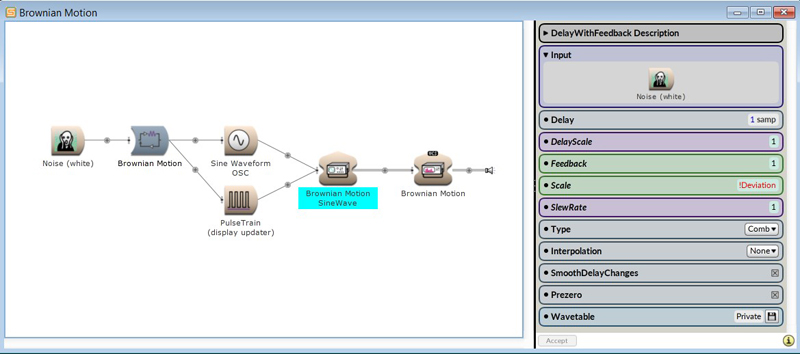
In this 1/f 2 frequency spectrum, a more pronounced modulation path can be seen. This Brownian noise is a random walk noise. Its spectral density is inversely proportional to f 2:
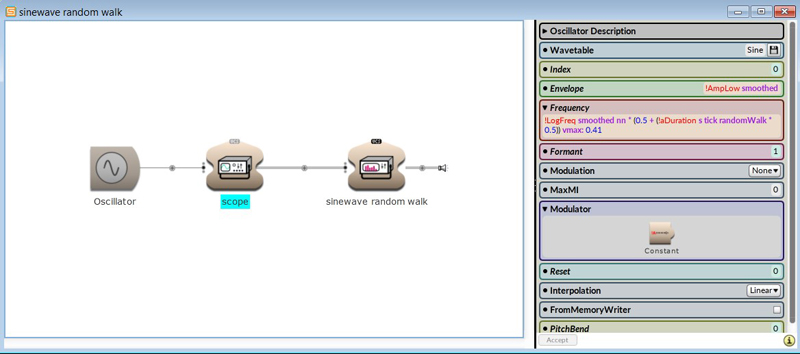
A more comprehensive way with an accelerated improvisation:
Discover more ways to create noise
It is important to create a toolbox of options to choose from. Different types
of noise have different expressions that we need to explore.
A stack of sinusoidal oscillators is the oscillator bank. The Frequencies and
Amplitudes fields both expect arrays of values, as each part of the spectrum can
have its own amplitude and frequency.
The number of values in the array should match the number in the Partials field.
Each oscillator follows a slow, random trajectory:
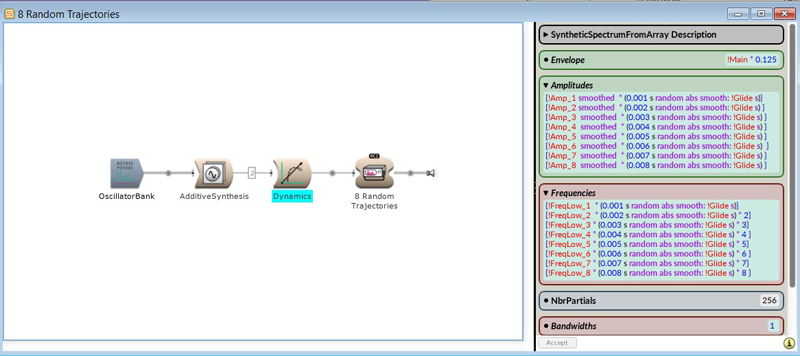
Next level noise generation
Random impulses as noise. By accelerating these impulses as points in time-space, the noise is formed by compression:
By moving these particles to different locations in
space, the energy and frequency of each particle changes the colour content of
the noise.
A spectacular view of beautiful possible spectral variations:
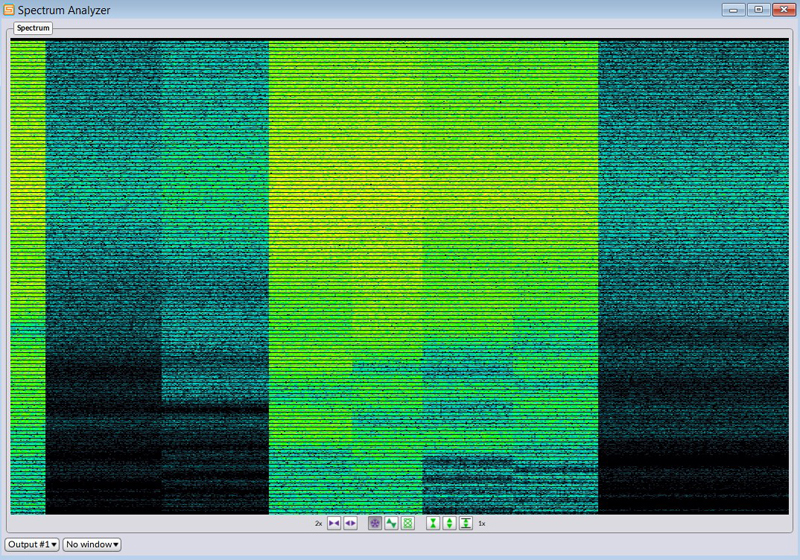
The use of an array of elements as a language in sample space:
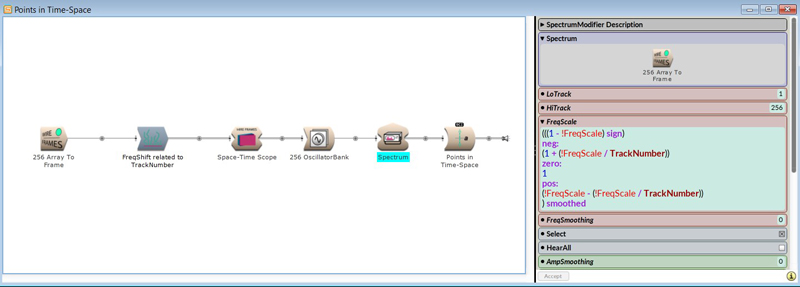
The spectral representation of the 256 elements used to generate noise. Each element, called a TrackNumber, can be shifted in time, creating different frequencies. In this way, tuned clusters of sine waveforms can be created and modelled in sample space.
By randomly measuring this arrangement of 124 elements, spread and bundled sine waves can be generated:
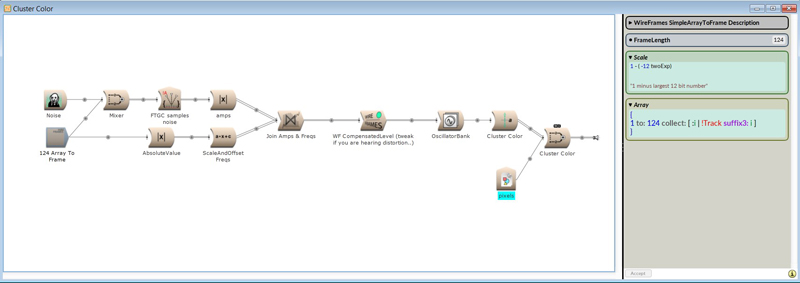
The elements are distributed over 124 points in the
pattern space, but are not static. The motion is generated by an image data
stream that is converted to white noise as random modulation.
Connect the dots:
Windowed particles provide a clear enunciation to shape this type of noise as a composition on a micro level.
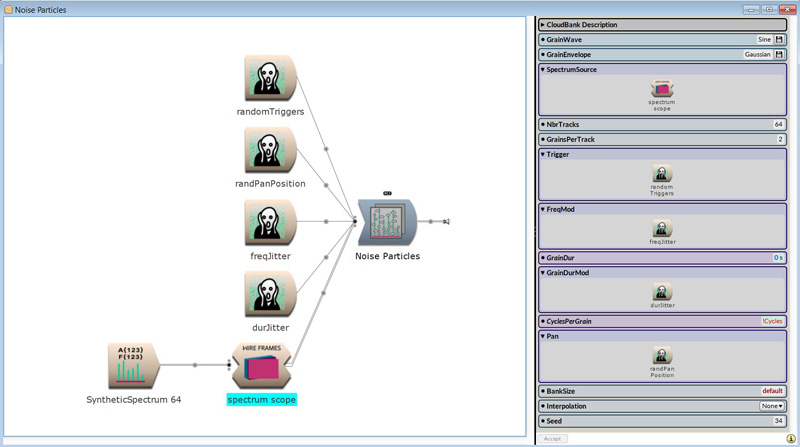
A window is a shape that models or envelops the amplitude of a
sound. By changing the shape of the amplitude, different timbres become
possible.
A spectral view of small enveloped sounds:
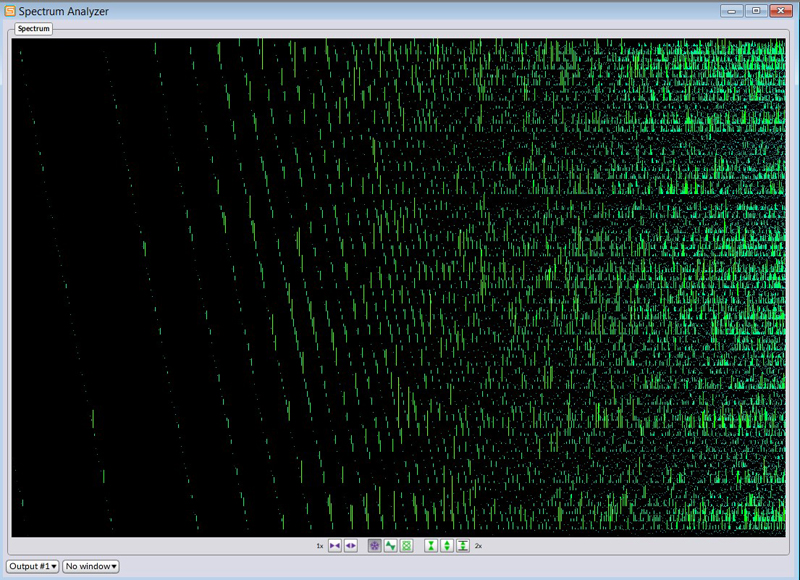
The same sound construction uses the Gaussian function for articulation. Instead of a sine wave, a wavetable with exponential noise was used.
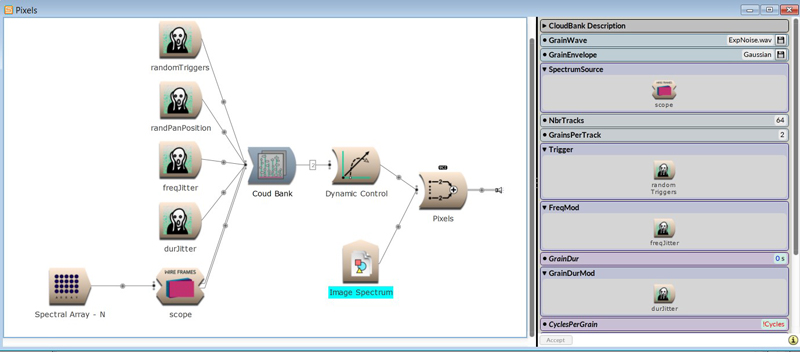
Noise can be assembled into a rapid palette of timbres:
Diffusing particles to colour
The colours in this sculpture are not pure yellow, red
and blue, we see colour gradients and transparent colour mixtures. Light
particles can be directed to form a gradient between the boundaries of each
colour, creating an x and y path in this 2D space. We can perceive
microdistances as interferences between particles.
It is interesting to investigate how a colour moves between the upper and lower
boundaries.
Stochastic movements between these boundaries can be constructed as a swarm,
where each sound window represents a colour pixel of the spectrum of that
specific colour.
Particles with yellow colour gradients:
Particles with red colour gradients:
Particles with blue colour gradients:
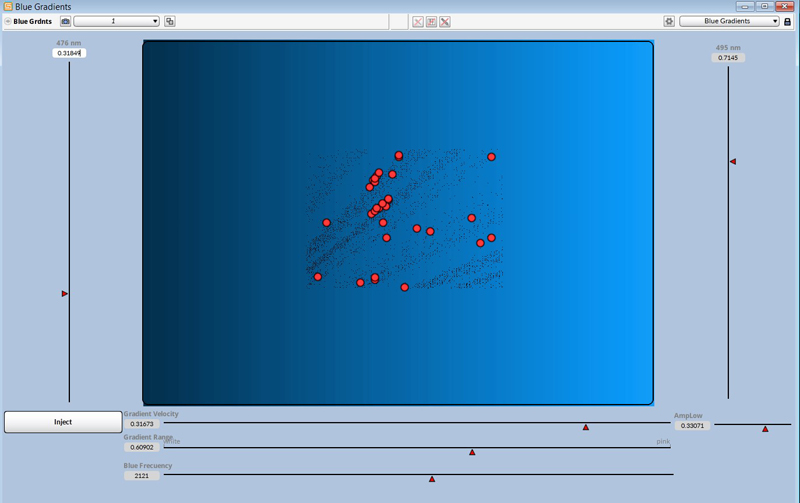
For each colour, stochastic sonic trajectories can be defined that create polymorphisms in the colour space of the colour gradients.
Spatial morphing
Windowed spectral boundaries for the colours yellow, red and blue. The morphings between the colours are created by merging the different windowed tone pixel colours.
Polymorphic for Leo Amino **
The sounds are produced by clustered forms of almagmatic, windowed noise.
The video consists of windowed colours in yellow, red and blue.
Windowing of transparent articulated colours through a Brownian noise that leads
to new random polymorphic forms.
It has become a canon of Amino's art. Kyma colour study in transparency:
** This is a part of a chapter from “NOISE: The Concept of Everything“, by Roland Kuit
Copyright © 2022 Roland Kuit
Your work is an exemplar of what is meant by “experimental music”. Your systematic, exploratory approach and careful documentation demonstrate the process of hypothesis, testing, and validation. This process is essential to “discovering/creating” new kinds of structures and procedures for the future of music. So few people understand and practice this approach to experimental music (many people conflate the mere use of technology with experimental music, but those are orthogonal!) - Carla Scaletti
Copyright © 2012 - 2024 Roland Emile Kuit. SONIC CULTURES LAB - SONIC SPACES, SONIC MANIFEST, Laboratory of Patching and SoundLab are trademarks of Roland Emile Kuit. All Rights Reserved. Unauthorized duplication and distribution of copyrighted material violates Federal Law. This website collects no personal data.